24. Gradient Descent
Gradient Descent
In this lesson, we'll learn the principles and the math behind the gradient descent algorithm.
Gradient Descent
Gradient Calculation
In the last few videos, we learned that in order to minimize the error function, we need to take some derivatives. So let's get our hands dirty and actually compute the derivative of the error function. The first thing to notice is that the sigmoid function has a really nice derivative. Namely,
\sigma'(x) = \sigma(x) (1-\sigma(x))
The reason for this is the following, we can calculate it using the quotient formula:

And now, let's recall that if we have
m
points labelled
x^{(1)}, x^{(2)}, \ldots, x^{(m)},
the error formula is:
E = -\frac{1}{m} \sum_{i=1}^m \left( y_i \ln(\hat{y_i}) + (1-y_i) \ln (1-\hat{y_i}) \right)
where the prediction is given by
\hat{y_i} = \sigma(Wx^{(i)} + b).
Our goal is to calculate the gradient of
E,
at a point
x = (x_1, \ldots, x_n),
given by the partial derivatives
\nabla E =\left(\frac{\partial}{\partial w_1}E, \cdots, \frac{\partial}{\partial w_n}E, \frac{\partial}{\partial b}E \right)
To simplify our calculations, we'll actually think of the error that each point produces, and calculate the derivative of this error. The total error, then, is the average of the errors at all the points. The error produced by each point is, simply,
E = - y \ln(\hat{y}) - (1-y) \ln (1-\hat{y})
In order to calculate the derivative of this error with respect to the weights, we'll first calculate
\frac{\partial}{\partial w_j} \hat{y}.
Recall that
\hat{y} = \sigma(Wx+b),
so:
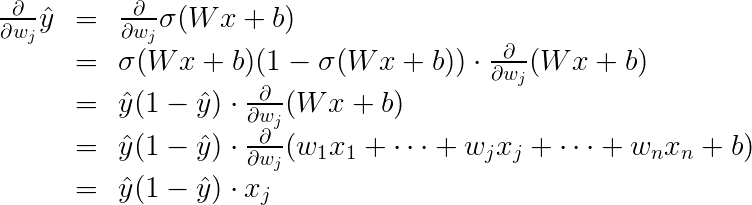
The last equality is because the only term in the sum which is not a constant with respect to
w_j
is precisely
w_j x_j,
which clearly has derivative
x_j.
Now, we can go ahead and calculate the derivative of the error
E
at a point
x,
with respect to the weight
w_j.
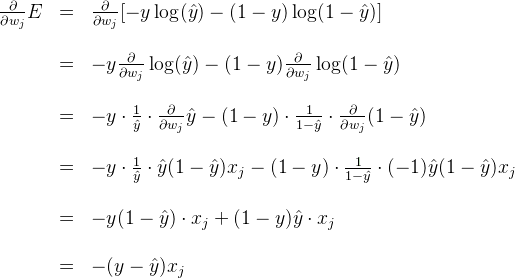
A similar calculation will show us that
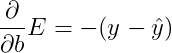
This actually tells us something very important. For a point with coordinates
(x_1, \ldots, x_n),
label
y,
and prediction
\hat{y},
the gradient of the error function at that point is
\left(-(y - \hat{y})x_1, \cdots, -(y - \hat{y})x_n, -(y - \hat{y}) \right).
In summary, the gradient is
\nabla E = -(y - \hat{y}) (x_1, \ldots, x_n, 1).
If you think about it, this is fascinating. The gradient is actually a scalar times the coordinates of the point! And what is the scalar? Nothing less than a multiple of the difference between the label and the prediction. What significance does this have?
SOLUTION:
- Closer the label to the prediction, smaller the gradient.
- Farther the label from the prediction, larger the gradient.
So, a small gradient means we'll change our coordinates by a little bit, and a large gradient means we'll change our coordinates by a lot.
If this sounds anything like the perceptron algorithm, this is no coincidence! We'll see it in a bit.
Gradient Descent Step
Therefore, since the gradient descent step simply consists in subtracting a multiple of the gradient of the error function at every point, then this updates the weights in the following way:
w_i' \leftarrow w_i -\alpha [-(y - \hat{y}) x_i],
which is equivalent to
w_i' \leftarrow w_i + \alpha (y - \hat{y}) x_i.
Similarly, it updates the bias in the following way:
b' \leftarrow b + \alpha (y - \hat{y}),
Note:
Since we've taken the average of the errors, the term we are adding should be
\frac{1}{m} \cdot \alpha
instead of
\alpha,
but as
\alpha
is a constant, then in order to simplify calculations, we'll just take
\frac{1}{m} \cdot \alpha
to be our learning rate, and abuse the notation by just calling it
\alpha.